type
status
date
slug
summary
tags
category
icon
password
KMP
pattern match问题,判断T是否是S的子串,其中T被称为pattern
BF
如果采用暴力算法会怎么样?
算法的基本思想是从主串的第一个字符开始和模式串的第一个字符进行比较,若相等,则继续比较二者的后续字符;否则,模式串回退到第一个字符,重新和主串的第二个字符进行比较。如此往复,直到主串中所有字符比较完毕。
设n为主串的长度,m为模式串的长度。默认n>=m,算法的时间复杂度O(mn)
暴力算法明显无法使人满意,在比较过程中有大量的浪费
前缀函数与KMP算法
前缀函数
给定一个长度为n的字符串s,其 前缀函数 被定义为一个长度为n的数组π[i]。 其中π[i]的定义是:
- 如果子串s[0..i]有一对相等的真前缀s[0...k−1]与真后缀s[i−(k−1)..i],那么π[i]就是这个相等的真前缀 (或者真后缀,因为它们相等) 的长度,也就是π[i] = k;
- 如果不止有一对相等的,那么π[i]就是其中最长的那一对的长度;
- 如果没有相等的,那么π[i] = 0。
特别地,规定π[0] = 0
举例来说,对于字符串
abcabcd,π[i] = [0,0,0,1,2,3,0]生成前缀函数
BF:时间复杂度
- 用j来寻找真前缀与真后缀相等的情况
- 从当前子串长度i开始,逐步减小
优化:
一个重要的观察是相邻子串前缀函数值至多增加1
- 所以当我们移动到下一个字串s[0..i]时,不需要令j=i
- j只有可能增加1,不变,或者减少
- 这样优化后算法的时间复杂度是
用数学语言描述,当s[i+1] = s[π[i]]时π[i+1] = π[i] + 1。这个式子的意思是,当我们移动到下一个子串时,新增的字符和原本子串找到的真前缀后一个字符是相同的,这样原本子串的真前缀和真后缀向后加一个字符,仍然相等。
可以看到,我们用上述关系能很方便地计算j,那么当s[i+1] ≠ s[π[i]],也就是失去匹配时或许也有类似的方法?
答案是可以找仅次于π[i]的第二长度的j,在这一长度的j有相同的真前缀和真后缀,然后再利用上述性质:当s[i+1] = s[π[i]]时π[i+1] = π[i] + 1,如果s[i+1] ≠ s[π[i]],则重复本规则寻找更小的j。
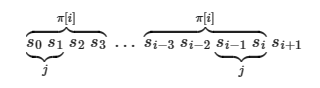
当找到了第二长度的j,他将满足如下关系:
s[0...j−1] = s[i−j+1...i] = s[π[i]−j...π[i]−1]
j等价于子串s[0...π[i]−1]的前缀函数值,即是j = π[π[i]−1],事实上π[i]的值正代表着相等的真前缀与真后缀的长度,那不就是j吗,因此得到j的状态转移方程:
jn = π[jn − 1−1](关键)
最终优化版本如下,不包含任何字符串比较:时间复杂度O(n)
KMP算法实现
给定文本t和模式串s,找到s在t中的所有出现;假设模式串长度为n,文本串长度为m。
思想:
- 构造字符串s+#+t,其中#是两字符串均不包含的分隔符
- 对这个连接起来的新字符串,求前缀函数即可
- 当π[i] = n,这说明找到了t的一个出现,且出现的右端点为i
- 该算法的时间复杂度O(n+m)
代码示例:
不论是生成前缀函数,还是前缀函数的应用即KMP算法,他们都抓住了字符串的特征,来避免多余的操作,同时它们都是在线算法,也就是你可以输入一个字符计算一下,再输入一个字符再计算一下,这对减轻空间开销十分有意义。
BM:Boyer-Moore算法
BM算法是对KMP算法的改进,通过引入坏字符表来进行更大跨度的跳转,进一步减小了时间浪费。
原理
核心思想仍然是通过模式字符串中的信息跳过子字符串的比较,BM算法加入了两个核心概念:坏字符和好后缀。
匹配过程
- 从尾部开始比较!
- 当出现失配时,我们称文本串中的这个失配字符为坏字符
- 文本串中出现了模式串中没有的那个坏字符,则将模式串整体移动到坏字符后方一个字符。
- 文本串中出现了模式串中有的坏字符,则将模式串中最靠右的对应字符与坏字符相对。
- 好后缀:所有尾部匹配的字符串,都是好后缀
- 好后缀移动规则:将模式串中好后缀上一次出现的地方与文本串中的好后缀对齐
- 好后缀移动规则要与坏字符移动规则相比较,取移动范围大者进行移动操作
实际例子:
Aho-Corasick
AC自动机,简单来说,这是KMP算法拓展到多模式后的结果。
单字符串->字典树(trie);Next数组->失配路径。
字典树与DFA
字典树原则:
- 根节点不含有字符
- 根节点到某一个终点连接起来为搜索字符串
- 任意节点的所有子节点包含字符不相同
使用字典树进行搜索符合有限自动机的概念。
原理
具体匹配时,需要引入失配指针的概念,显然,如果一个字符失配了,我们不一定要重新开始匹配。失配指针的构建方法如下:关键在于,如果father的fail能够接纳自己,比如这里8号节点的father的fail也就是0号节点,可以接纳h,那么我们就将8号节点的fial指向接纳h后的1号节点。如果没有满足的条件,则继续回溯father‘s father的fail,一直都没有的话就指向根节点。
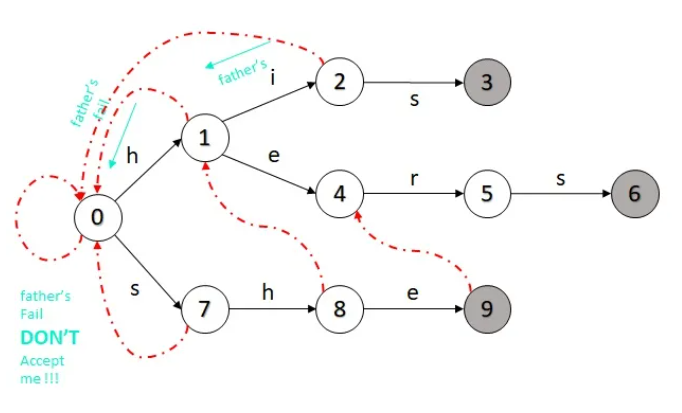
- root指向自己
- father是root则指向root
- 回溯判断father的fail
- if father的fial节点能够接纳自己,then指向father的fial节点接纳自己后的节点
- else 继续回溯father’s father的fial节点
- 如果回溯到根节点还没有找到,那就把fial节点指向根节点
构建完毕后匹配的过程就很简单了,直接由根节点一路往下查询即可,如果失配,依照fail指针进行回溯。
Wu-Manber
WM算法是一种多模式匹配算法,它是上文所述AC算法的优化。
原理
VM算法的构成如下:SHIFT,HASH,PREFIX。
一般从模式串集合中,所有模式的前m个字符构建SHIFT表,其中m是模式串集合中最短模式的长度值。我们可以把这前m个字符称作前缀。
构建SHIFT表的过程是:
- 在前缀中取一个一个字符快B,字符快B的长度一般为2或者3,计算它与前缀末尾的距离n。
- 以模式abcdefgh为例,假设m=6,那么SHIFT[ab]=4,SHIFT[bc]=3,SHIFT[cd]=2,SHIFT[de]=1,SHIFT[ef]=0都要加入SHIFT表中。
- 如果一个模式或者多个模式中有相同的字符快,选取SHIFT值小者加入SHIFT表。
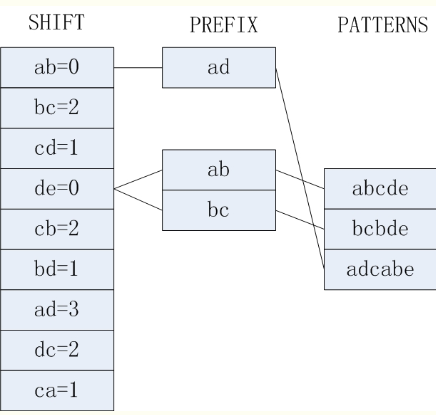
构建完SHIFT表后我们构建HASH表,即将所有SHIFT[B]=0的表项映射到对应的模式串,比如对于m=5时模式串abcde,bcbde,对于块de,他们的SHIFT值都是0,所以他们都由de索引。
其实构建完以上两个表已经可以进行匹配了,但是为了应对一个SHIFT表项可能索引非常多个模式串的情况,比如,有10个以de结尾的模式串就会十分不方便,因此建立PREFIX表,存储模式串的第一个字符块(或者说存储一定长度的PREFIX前缀)。
匹配过程
对于目标串target,游标i,模式前缀长度m,字符快长度B,PREFIX前缀长度C(在这个例子中就是取出的第一个字符快)
- 对于target[1…n],初始游标置于i=m处
- 我们取target[i-B+1…i](以i结尾的字符快),查找其在SHIFT表中的对应值SHIFT[target[i-B+1…i]]
- 如果找不到,则i+=m-B+1。在B=2的情况下就是m-1
- 如果其值为c(c != 0),那么我们i+=c,再执行上述操作
- 如果其SHIFT值等于0,我们需要取出target[i-m+1…i-m+C](前缀m中的第一个字符快),然后在SHIFT[de]=0对应PREFIX结合中查找PREFIX[target[i-m+1…i-m+C]]
- 如果不存在,则将游标i+=1
- 如果存在则用target[i-m+1]开始的子串,依次匹配满足条件的所有模式串,直到找到匹配模式,或者未发现匹配位置。然后i+=1,继续向后查找
下面以WM算法对目标串target[1…10]=dcbacabcde,模式集合P{abcde,bcbde,abcabe},的匹配过程来形象的说明一下。首先,对于模式集合P预处理之后的结果如上面的程序结构图所示。然后从i=5开始执行算法。首先我们发现target[4…5] = ac,SHIFT表中不存在ac,所以i+4,到target[9],此时发现target[8…9]=cd,SHIFT[cd]=1,所以i+1,然后发现target[9…10]=0,我们取target[6…7]=ab,发现PREFIX[ab]对应的模式串是abcde,然后我们从target[6]开始用目标串与模式串比较,发现匹配模式abcde。
- 作者:jackpai
- 链接:https://www.jackpai.life//technology/algorithm-string-match
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。









